What are Lamport timestamps?
I wrote about the happened-before relation and about processes and messages in this model. Happened-before gives us a way to think about time and causality. But how can we measure those things?
“Lamport timestamps” are one method to measure time and causality. The idea is that each process/message carries a timestamp, and that we can compare these timestamps as a way to determine whether one event happened-before another (i.e., whether the first event could have caused the second). Consider the following process diagram:
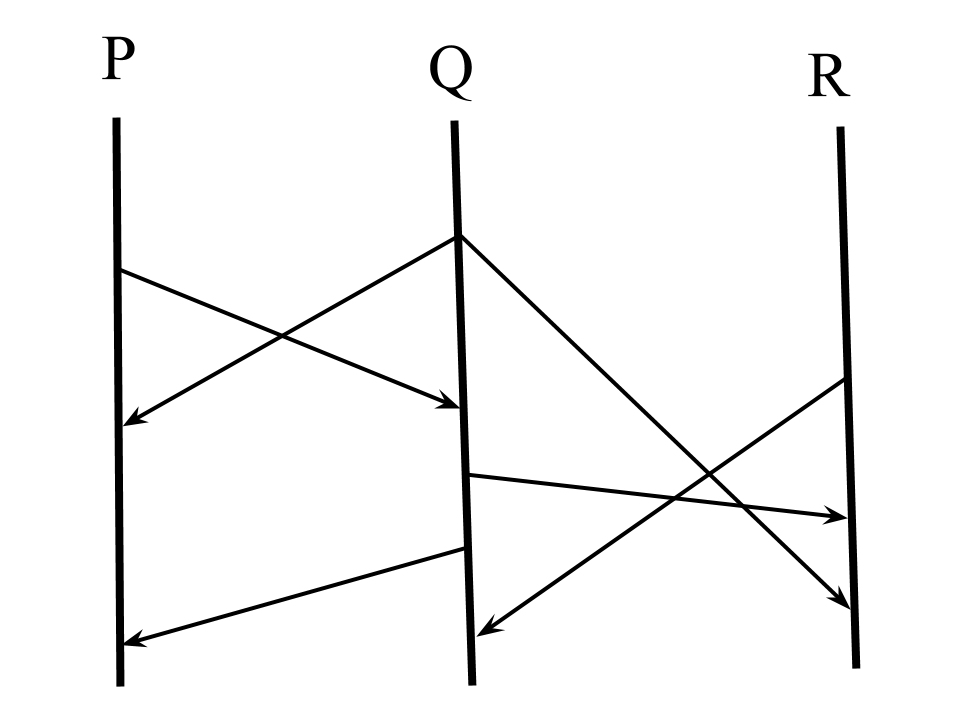
Lamport has us annotate each line in the diagram with a natural number (the timestamp), like so:

Each timestamp is generated from the previous ones. So for a sent message, the new process timestamp and the sent message timestamp are the result of the previous process timestamp. And for a received message, the new process timestamp is the result of the previous process timestamp and the inbound message’s timestamp.
The important property in these events is that the new timestamps are bigger than the old ones. From this, the algorithm is clear:
int timestamp;
void send_message(char* msg, int to) {
timestamp++;
write(to, mk_msg(msg, timestamp));
}
void on_receive_message(msg_t msg) {
timestamp = max(timestamp, msg.timestamp) + 1;
}For processes, you can see the timestamp as a monotonically increasing “last event timestamp”, and for messages, you can see the timestamp as an immutable “timestamp of the event that caused this message”. Events are sending messages or receiving messages. (We could add “internal process events” to this model, but Lamport chooses not to.) So the above diagram represents these event timestamps:

What’s the point of all this? The point is to separate events into layers:

These layers correspond to each’s process’s observation of the passing of time (i.e. “time” as interpreted by the happened-before relation). Similarly, we can see the timestamp as counting the longest path of events leading to this event.
What is the relationship between the Lamport timestamp and the happened-before relation? Formally, it’s that:
If event A happened-before event B, then the timestamp of A is less than the timestamp of B.
We can write “event A happened-before event B” as A → B, and “the timestamp of A” as T(A), so we can write
A → B ⇒ T(A) < T(B)
Why is this so? A → B means “B is reachable from A by following messages”. For each possible path from A to B, every step in the path increases the timestamp by at least one.
Is this property useful? Superficially, no, because we’d like the implication to go the other way. But the implication doesn’t work the other way. We can show that
T(A) < T(B) ⤃ A → B
We can see this by example: see the event 3 in process Q and the event 1 in process R. These events are concurrent by the happened-before relation (i.e., A ↛ B), but it’s not the case that 3 < 1.
However, we can use the implication in the contra-positive:
T(A) <= T(B) ⇒ B ↛ A
Or, in English, “If the timestamp of A is less than or equal to the timestamp of B, then B did not happen-before A.”
It should be clear that the relationship between the Lamport timestamp and the happened-before relation is not one-to-one, because timestamps are totally ordered (they’re natural numbers, using the ordinary < relation), whereas the happened-before relation only gives us a partial order, where events can be concurrent.
From equality of timestamps, we can conclude that two events are concurrent. That is:
T(A) = T(B) ⇒ A ↮ B
This is a consequence of the contra-positive.
In summary, by comparing timestamps, we get
T(A) < T(B) ⇒ B did not happen-before A (equivalently, A might have happened-before B)
T(A) = T(B) ⇒ A and B are concurrent
We can also see Lamport timestamps in a diagram which removes the process/message distinction.

Here, the algorithm is simpler:
To split a process, create two processes, each with timestamp T(P)+1
To join processes, create a new process with timestamp max(all timestamps)+1This page copyright James Fisher 2017. Content is not associated with my employer.
 Granola
Granola